
The slope of a line can be interpreted either as a ratio or proportion, or as a rate, rhythm or speed of change. Considering that if the axes x and y have the same unit of measurement, the slope is unitless and is a ratio or proportion.
If the x and y axes have different units of measurement, the slope is a rate, rhythm or speed of change.
All this definition makes us think that when studying calculus we can find applications related to both interpretations of slope.
Example of rate or speed of change
The population of a country in the American continent was 3687000 inhabitants in 1990, then in 2000 it became 4042000 inhabitants. Calculate:
a. The rate or speed of change during the period from 1990 to the year 2000.
b. If the population of the American country grows at the rate of change during the period from 1990 to 2000. Calculate the number of inhabitants for the next 10 years.
Solution to the exercise
To calculate the rate of change from 1990 to 2000, we apply the slope formula:

Where:
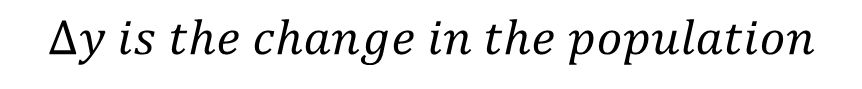
Therefore:


Therefore:
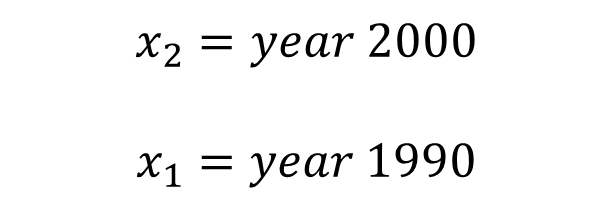
Now we calculate the slope which is the rate of change:
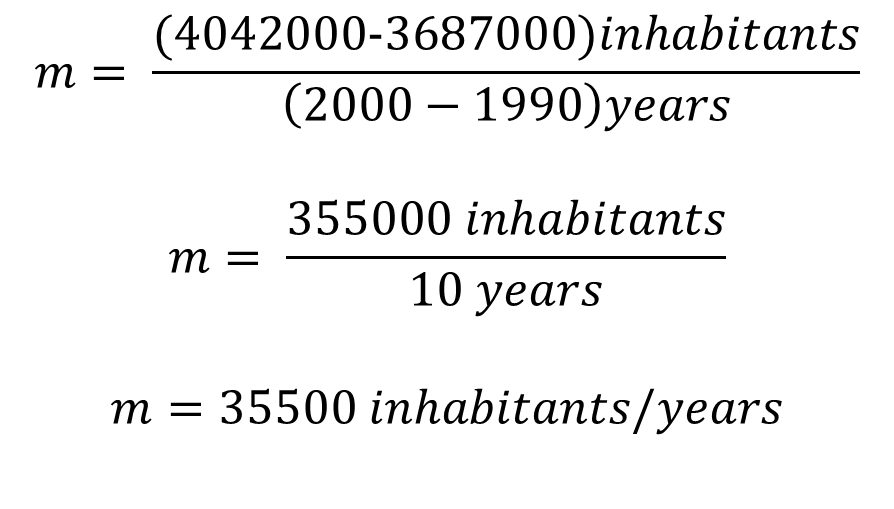
This means that the population grew at a rate or speed of change of 35500 people per year.
To calculate the population of the American country for the year 2010 considering the rate of change of 35500 inhabitants per year, we must start from the number of inhabitants for the year 2000, which is 4042000 inhabitants, to which we will add 355000 inhabitants which is the growth in 10 years, which gives us a result of 4397000 inhabitants.
Bibliographic Reference
Calculus with Analytic Geometry by Ron Larson, Robert, P. Hostetler and Bruce H. Edwards. Volume I. Eighth Edition. McGraw Hill. Año 2006