Crack the Riddle on His Tomb Stone to Know His History

This is a simple mathematical puzzle and is quite famous too. It is based on the life of Diophantus the mathematician who wrote Arithmetica. He is often called the father of algebra. Most of what we know about his life comes from this puzzle, sometimes referred to as his epitaph.
I have seen similar problems in competitive exams and quantitative aptitude tests. They are also asked in software & finance companies’ quant interview rounds. The time limit to solve such a question is usually 60 — 75 seconds. Can you solve it within this time limit?
Reminder: This is a word problem and you may get a wrong answer if in a hurry. So read it carefully.
So, get ready and let’s dive in!
Problem
Epitaph of Diophantus read:
“God gave him his boyhood one-sixth of his life, One twelfth more as youth while whiskers grew rife; And then yet one-seventh ere marriage begun; In five years there came a bouncing new son. Alas, the dear child of master and sage After attaining half the measure of his father’s life chill fate took him. After consoling his fate by the science of numbers for four years, he ended his life.”
In simpler words:
Diophantus’s boyhood lasted 1/6 of his life; his beard grew fully after 1/12 more; he married after 1/7 more, and his son was born 5 years later; the son lived to half his father’s age, and the father died 4 years after the son.
Determine how long Diophantus lived and identify his age at the time of other important events in his life?
You should pause here, grab your notebook and pen, and try to find the solution yourself. 🧠🤔
When ready, scroll down and read the solution provided!
Solution
We can start by assuming Diophantus’s age as x.
- Childhood: His boyhood lasted x/6.
- Full Beard: His beard grew fully after x/6 + x/7 years into his life.
- Marriage: He married after x/6 + x/7 + x/12 years into his life.
- Son’s Birth: His son was born 5 years after the marriage. So, x/6 + x/7 + x/12 + 5 years into his life.
- Son’s Lifetime: His son lived x/2 years.
- Diophantus’s Death: He passed away 4 years after his son’s death.
So, His Age = Death = His lifetime before his son + Son’s Age + 4.
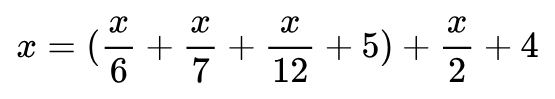
Final Answer
Solving the above equation gives x = 84. So he lived for 84 years.
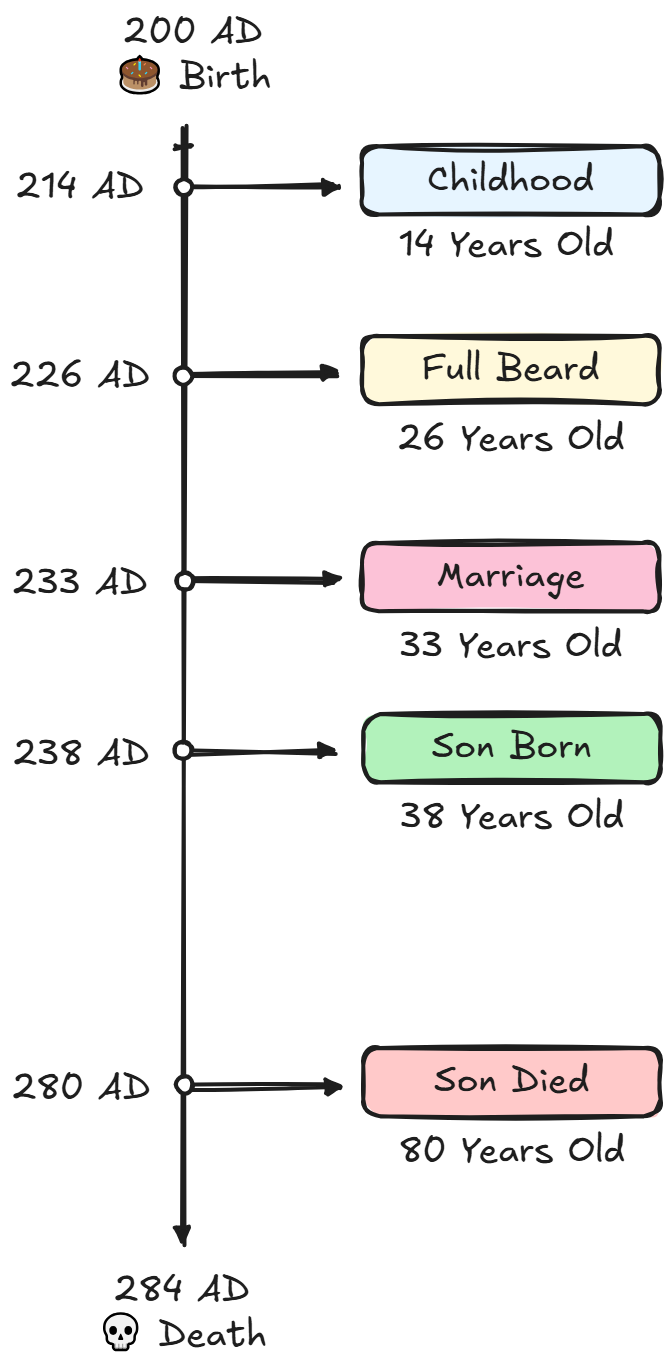
So the timeline of the major events of his life:
- Childhood lasted 84/6 = 14 years.
- First beard at 14 + 84/7 = 14 + 12 = 26 years.
- Marriage at 26 + 84/12 = 26 + 7 = 33 years.
- Son was born when he was 33 + 5 = 38 years.
- His son lived 84/2 = 42 years and passed away when Diophantus was 38 + 42 = 80 years old.
- Diophantus died at 80 + 4 = 84 years old.
Illustration
There is not much clarity about his birth but assuming he was born in 200 AD:
 )
)If you found this interesting, feel free to like, comment or follow me. We all go further when we help each other!
Cheers — RS !!
Posted Using INLEO