In my previous post I shared the work from a number of different thinkers I have recently come across, all of which who seem to have conepts centered around a common geometric shape.
In this post we will broaden the subject from simply noticing this pattern and begin to explore some of the inner workings of this shape. Some of the running themes through this will be electromagnetism, vibration, and frequency. We will delve into the subjects of spherical harmonics as well as cymatics, touching briefly on sacred geometry. Finally we will wrap up by discussing energy-matter conversion and the formation of matter.
Before we dive in, let's quickly refresh our memory from the opening video in my previous post.
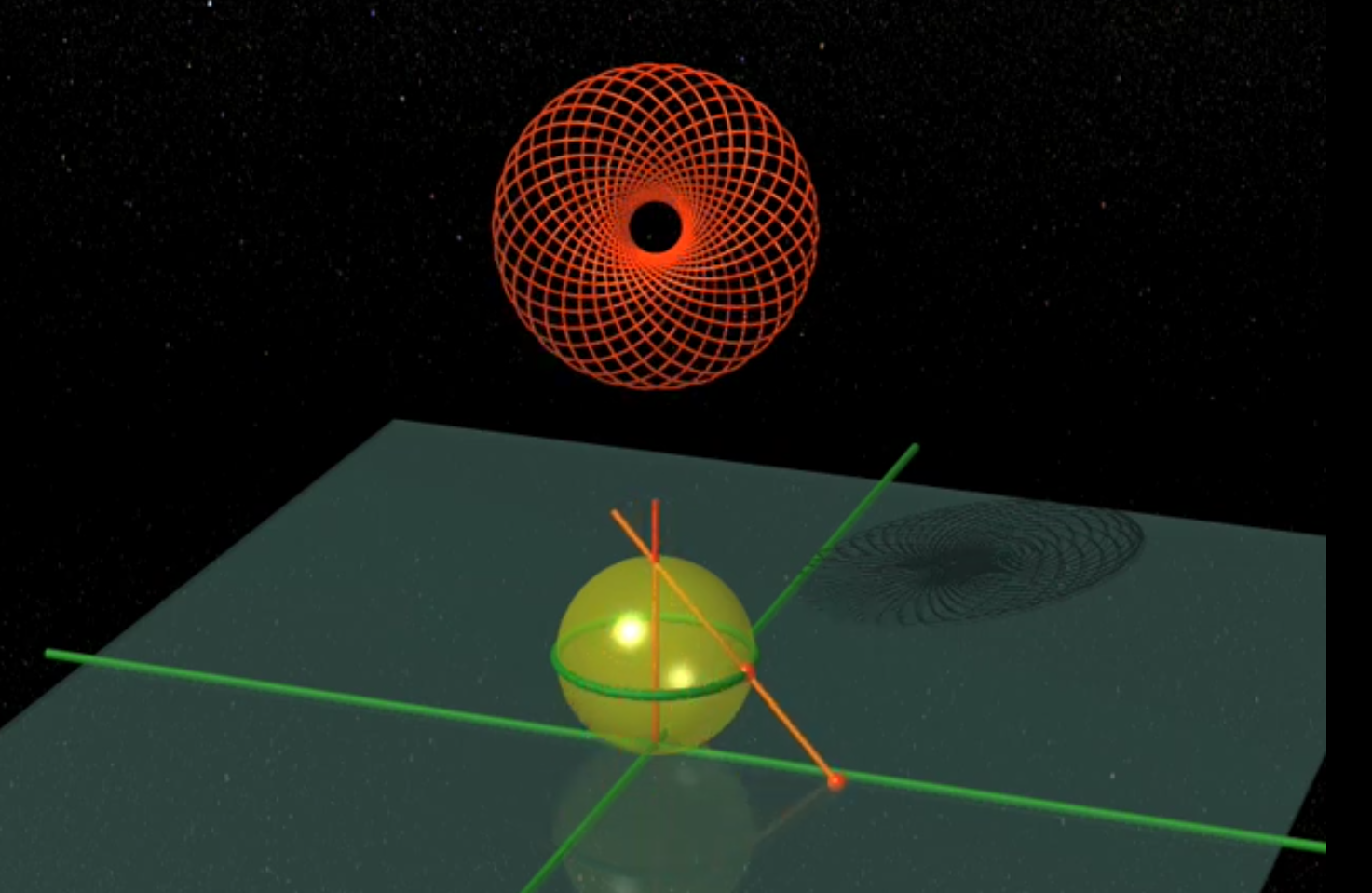
You may recount that as the torus "slid" up or down on the sphere, a new nested torus would be drawn. Let's keep these fourth dimensional "happenings" in the back of our mind as we explore these additional concepts. The first video I want to share is on spherical harmonics. This will give us a way to visualize how waves interacts with these hopfion fields.
Spherical harmonics are like the fingerprints of waves rippling across a 4D hypersphere—our S³. They’re special functions (eigenfunctions, if you’re feeling fancy) that show how vibrations play out in this wild geometry. Each one comes with a number—an eigenvalue—that’s like its pitch or energy level, setting the “frequency” of these cosmic waves. In physics, we sometimes call these patterns eigenstates, especially in quantum mechanics, where they’re the possible “poses” a system can strike, each tagged with a specific energy or momentum.
Here’s what interesting, these eigenstates shape the fuzzy “probability clouds” around atoms. Each orbital’s shape—spherical, dumbbell, or cloverleaf—comes from a different flavor of spherical harmonic. Now, every atom doesn’t get its own unique shape collection; hydrogen, helium, and carbon all pull from the same shape toolbox (s, p, d orbitals). What changes is the energy and arrangement of their electrons, depending on the atom’s type and surroundings—like whether it’s solo or bonded up in a molecule.
Subatomic particles—like electrons, protons, or quarks—also have eigenstates, but these are usually defined in the context of a system (like an atom or a free particle).
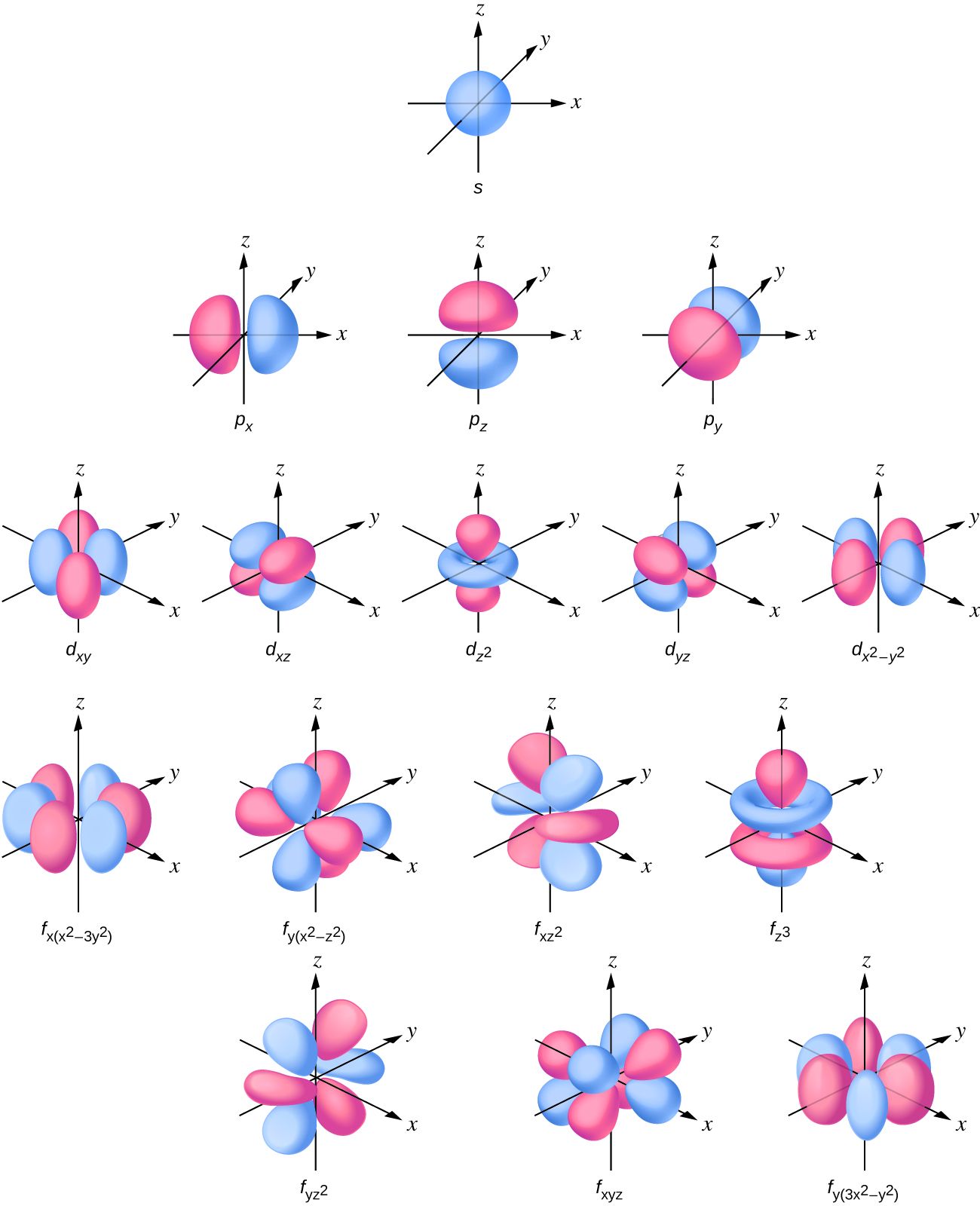
These orbital shapes and energies seem to hint at a deeper pattern. That’s where Walter Russell comes in, a thinker we touched on yesterday. He took a simple sine wave and spun it into a periodic table based on octaves and harmonics.
Normally in diagrams it is shown in a stretched out position to display everything clearly.
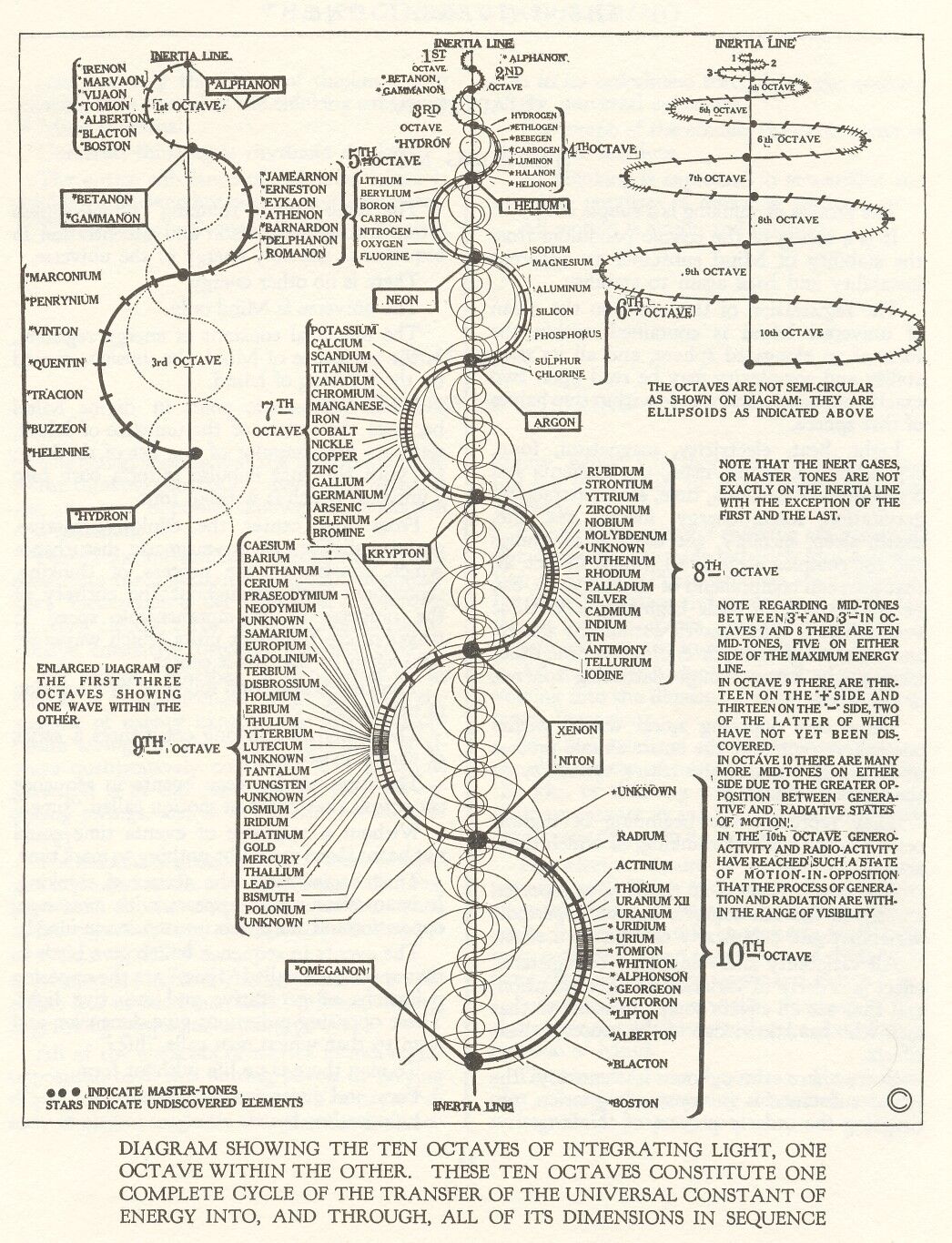
What's cool is you can take this stretched out sine wave and coil it up. When it is viewed from this perspective it looks like a spiral. We can take that spiral and map it onto the Clifford Torus and that is exactly what Malcolm Bendall has done.
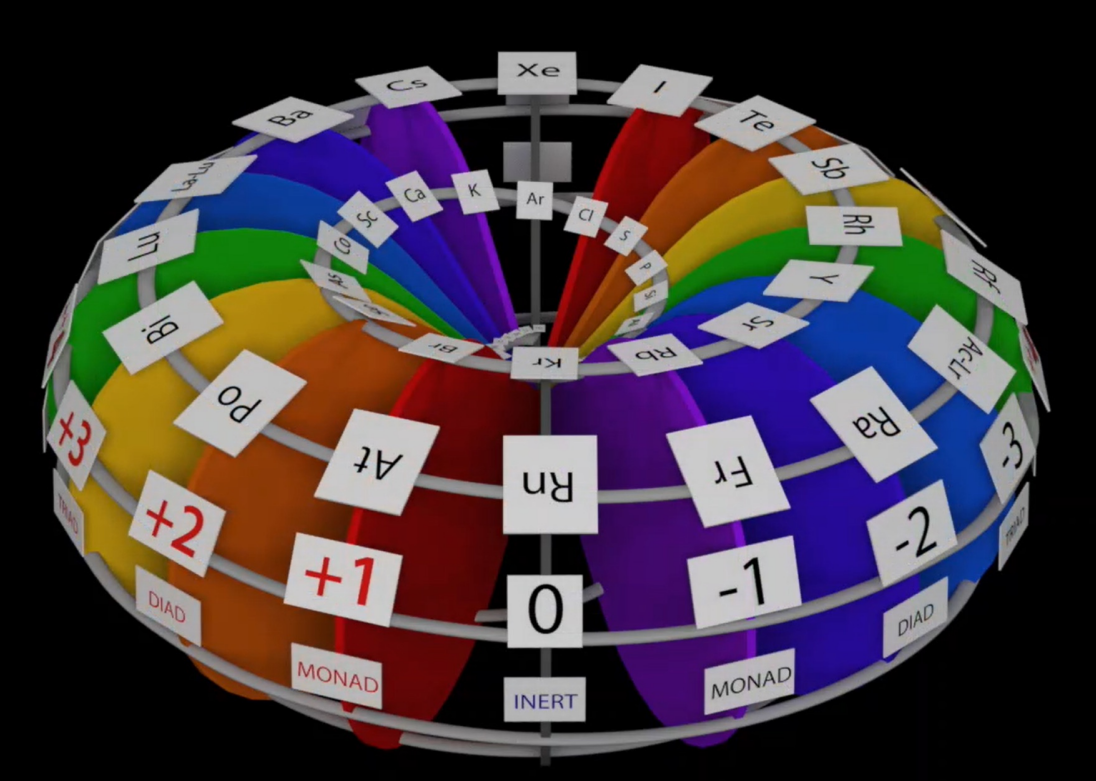
The Bendall Torus is a three-dimensional, toroidal model for arranging the periodic elements, distinct from the standard two-dimensional periodic table. It’s part of Malcolm Bendall’s Plasmoid Unification Model (PUM), which emphasizes resonance, charge density, and geometric harmony over traditional atomic number and electron configuration. Rather than hopfions, Bendall refers to these stable toroidal structures of charge density as Plasmoids. The torus is structured with eight intersecting planes at 22.5-degree angles (360° / 16, hinting at a 16-sector design) and incorporates a Sanskrit Fibonacci curve on a "100 Pi surface," where intersections with these planes define elemental positions.
This seamlessly leads us right into the work being done by Sheela Rahman in what she calls "Coherent Geometry".
In that video, Sheela provides a lecture on how she has taken the resonant frequencies out of Malcolm Bendall's Plasmoid Unification Model and analyzed them with an oscilloscope. She demonstrates how some frequencies can create a variety of stable patterns while others make scrambled unharmonious patterns.
Also you may recall the videos from yesterday on Primer Fields, we saw lab experiments using unmagnetized steel balls stand in for how the energy flows through this toroidal structure. In those demonstrations we saw energy concentrate more densely toward the "nucleus". When under the influence of the Primer Fields the steel balls gained an electric charge and thus would have a magnetic field reminiscent to the Coulomb force.
You can see the steel balls self-organize into a crystalline lattice.

Although not visible to the eye, these balls are being held together yet repelled from one another, by the hopfion fields (LaPoint calls them Primer Fields). It is said that this interaction of electromagnetic forces are the true culprit behind what is commonly referred to as the strong force.
To finalize the segment of my thoughts lets quickly recap. Spherical harmonics on the 3-sphere create nested tori. Each of those tori have a natural resonant frequency. Some resonant frequencies create stable patterns and other do not. Energy that gets concentrated at the nucleus becomes electrically charged and exhibit Coulomb Force-like behavior.